On day 1, one person discovers a secret.

You are given an integer delay, which means that each person will share the secret with a new person every day, starting from delay days after discovering the secret. You are also given an integer forget, which means that each person will forget the secret forget days after discovering it. A person cannot share the secret on the same day they forgot it, or on any day afterwards.

Given an integer n, return the number of people who know the secret at the end of day n. Since the answer may be very large, return it modulo 10^9 + 7.

題目說有一個人在第一天發現了一個秘密。
有兩個整數delay、forget，
分別表示人會在發現秘密後的delay天開始與另一個人分享這個秘密；
與人在發現秘密後的 forget 天會忘記這個秘密。一旦某人忘記秘密，他們將無法再分享秘密。
咱的目標是返回在第n天知道秘密的人數。
題目還提到答案可能非常大，要將結果對10^9+7取模。雖然我還沒get到這句話的含義，但我知道這會是場硬戰。

我的解題思路：

• 做一個動態矩陣 share[i] 表示第i天可以分享秘密的人
• 第i天知道秘密的人會在第 i+delay 天影響 day[i + delay]
• 但這些人在第 i+forget 天不再影響後續分享，自身也不再記得秘密。
• 第n天知道秘密的人是從第 n-forget+1 天到第 n 天知道秘密的人
• 「取模」就是取除法的餘數，當計算結果很大時，將其對一個數字取模，可以保證結果維持在一個範圍內。
• Mod要在每個運算後面都加

1. 從第一天開始遍歷，直到第n天
2. 計算每天可以分享秘密的人，並減去忘掉的人
3. 返回取模後的第 n-forget+1 天到第 n 天知道秘密的人總和

因為答案一直錯誤，改到後來程式已經亂七八糟了！！
於是參考了大神分享的正解，再修改原本的程式...
邏輯基本上是一致的，不過它在每一天，是從 i-delay 天前開始計算分享的人數，
然後減去從 i-forget 天前開始忘記的人的數量。
這樣可以確保只有在有效的時間範圍內計算。

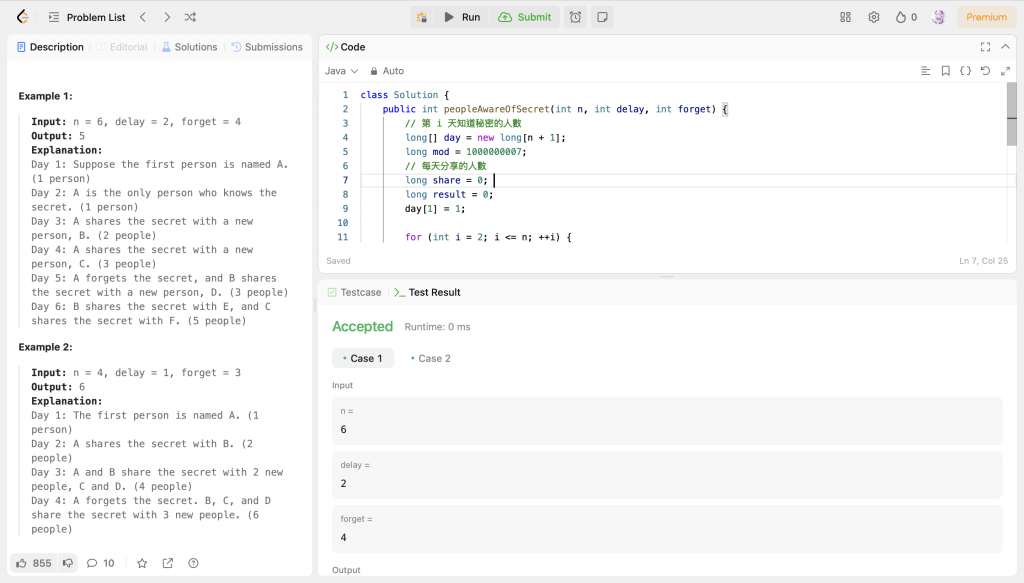
class Solution {
    public int peopleAwareOfSecret(int n, int delay, int forget) {
        // 第 i 天知道秘密的人數
        long[] day = new long[n + 1]; 
        long mod = 1000000007;
        // 每天分享的人數
        long share = 0; 
        long result = 0; 
        day[1] = 1; 

        for (int i = 2; i <= n; ++i) {
            // 計算今天分享的人數
            share = (share + day[Math.max(i - delay, 0)] - day[Math.max(i - forget, 0)] + mod) % mod;
            day[i] = share; // 更新今天知道秘密的人數
        }

        // 計算最後知道秘密的人數
        for (int i = n - forget + 1; i <= n; ++i) {
            result = (result + day[i]) % mod;
        }

        return (int)result; // 返回結果
    }
}

結束這回合！！！！！！！